https://www.acmicpc.net/problem/2159
2159번: 케익 배달
첫째 줄에 N이 주어지고 둘째 줄에는 선아가 일하는 레스토랑의 위치가, 셋째 줄부터는 N명의 위치가 X와 Y로 주어진다. 두 좌표 사이에는 공백이 하나 이상 있다. (1 ≤ N, X, Y ≤ 100,000)
www.acmicpc.net
안녕하세요 블로그 첫 글이네요 하하하 오늘은 DP를 활용한 Gold 2 문제 케익 배달을 풀어보았습니다.
1. 문제
프랑스에서 공부를 하고 돌아온 선아는 자신이 그렇게도 되고 싶어 했던 파티셰가 되었다. 케익 배달 전문업체 보나뻬띠에 취직한 선아는 친절하게도 자신이 만든 케익을 고객들에게 직접 배달을 하려 한다. N명의 고객에게 케익을 배달하는데 주문이 들어온 순서대로 배달하기를 원하며 고객이 케익을 받을 수 있을 만큼 충분히 가까이까지 배달한다.
N명의 고객의 위치는 순서대로 100,000×100,000 격자의 정수 좌표로 주어지고 처음 출발하게 되는 보나뻬띠의 위치도 정수 좌표로 주어진다. 선아는 격자 위에서 상하좌우로만 움직이며 고객에게 케익을 전달하기 위해서는 그 고객의 위치까지 가거나 고객의 상하좌우 인접 격자점에 가야 한다. 이때 선아가 최단거리를 이동하여 입력된 순서대로 배달을 끝낼 수 있는 거리를 계산하는 프로그램을 작성하시오. 여기서 거리는 격자 상의 칸 수를 말한다.
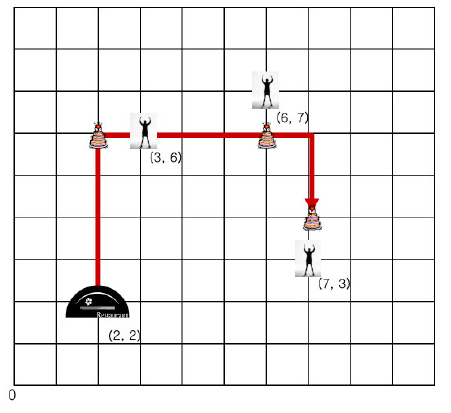
위의 예에서 선아는 11칸을 움직여서 세 명의 고객에게 배달을 마칠 수 있다. 선아는 반드시 고객들에게 순서대로 배달을 하며 순서에 어긋난 사람에게 배달을 할 수 있는 위치에 있더라도 케익을 주지 않고 순서대로 배달을 한다. 고객의 위치는 중복이 될 수도 있다.
2. 풀이
좌표평면 상의 최단거리를 구하는 문제이기 때문에 기본적으로 DFS, BFS를 떠올릴 수 있습니다만
단순 그래프 탐색을 한다면 한 고객 당 고려해야 할 지점이 5개이기 때문에 대강 O(5^n) 이라는 어마무시한 exponential 시간 복잡도가 기다리고 있겠습니다.
여기서 핵심은 현재 고객 주위 5지점에서 다음 고객 주위 5지점 까지의 경우의 수는 25가지이고 이 값은 고정적이기 때문에 이를 dp 배열에 저장해두면 중복 계산을 피할 수 있습니다.
3. 코드
아래 코드는 Top-down 방식이며
dp[idx][n]은 idx번째 고객 주위 n번째 지점에서 부터 마지막까지 배달하는 최소 경로의 길이 입니다.
//https://www.acmicpc.net/problem/2159
//2159. 케익 배달(Gold2, DP, DFS)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
#define endl "\n"
#define INT_INF 2147483647
#define LL_INF 9223372036854775807
#define ll long long
using namespace std;
int N;
pair<int, int> loc[100001];
int dx[5] = {0, 1, -1, 0, 0};
int dy[5] = {0, 0, 0, 1, -1};
ll dp[100001][5];
ll cal(int x, int y, int idx, int n) {
if(idx == N) return 0;
ll &ret = dp[idx][n];
if(ret != -1) return ret;
ret = LL_INF;
for(int i = 0; i < 5; i++) {
int nx = loc[idx + 1].first + dx[i];
int ny = loc[idx + 1].second + dy[i];
if(nx < 1 || nx > 100000 || ny < 1 || ny > 100000) continue;
int dist = abs(nx - x) + abs(ny - y);
ret = min(ret, dist + cal(nx, ny, idx + 1, i));
}
return ret;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
freopen("input.txt", "r", stdin);
//INPUT
cin >> N >> loc[0].first >> loc[0].second;
for(int i = 1; i <= N; i++) {
cin >> loc[i].first >> loc[i].second;
}
//SOLVE
memset(dp, -1, sizeof(dp));
cout << cal(loc[0].first, loc[0].second, 0, 0);
//OUTPUT
}
아래 코드는 Bottom-up 방식이며
dp[idx][n]은 idx번째 고객 주위 n번째 지점까지 가는 최소 경로의 길이입니다.
memset(dp, 0, sizeof(dp));
for(int i = 1; i <= N; i++) {
for(int j = 0; j < 5; j++) {
dp[i][j] = LL_INF;
for(int k = 0; k < 5; k++) {
int cx = loc[i].first + dx[j];
int cy = loc[i].second + dy[j];
int px, py;
if(i == 1) {
px = loc[i-1].first;
py = loc[i-1].second;
} else {
px = loc[i-1].first + dx[k];
py = loc[i-1].second + dy[k];
}
if(cx < 1 || cx > 100000 || cy < 1 || cy > 100000) continue;
if(px < 1 || px > 100000 || py < 1 || py > 100000) continue;
dp[i][j] = min(dp[i][j], dp[i-1][k] + abs(cx - px) + abs(cy - py));
}
}
}
//OUTPUT
ll ans = LL_INF;
for(int i = 0; i < 5; i++) {
ans = min(ans, dp[N][i]);
}
cout << ans;부족한 첫글 읽어주셔서 감사하고
화끈한 지적이나 질문 언제든 환영합니다 감사합니다~!
'알고리즘 > 백준' 카테고리의 다른 글
| [백준/BOJ] 10986번 - 나머지 합[C++] (0) | 2023.03.08 |
|---|---|
| [백준/BOJ] 23817번 - 포항항[C++] (0) | 2023.02.21 |
| [백준/BOJ] 17780번 - 새로운 게임[C++] (1) | 2023.02.01 |
| [백준] 2437번 - 저울[C++] (2) | 2023.01.17 |
| [백준] 2216번 - 문자열과 점수[C++] (0) | 2023.01.12 |